mathematics

Beauty in irrationality?

Plotting irrational numbers (pi, e, sqrt2, golden ratio) as vectors allows their complexity to be visualised

I have always wanted to visualise irrational numbers. Our brains are capable of recognising patterns in nature and I wanted to know if these patterns could be visualised in irrational numbers, and whether beautiful patterns could be seen that could lead to an further understanding of the irrational nature of the numbers. Just found out after publishing this article that the idea has been round for a while! (here is an interesting blog article). Here I have extended the technique to 3 dimensions for better visualisation and give results and computer code.

Experimental Technique

In this experiment the fractional parts of the irrational numbers, pi, e, sqrt2 and golden ratio are transformed into vectors in cartesian space for visualisation purposes. Each digit of the number sequence (from left to right) is transformed into a spatial vector with unit length. The orientation is calculated from the number as: angle = (digit/10)*2*pi. Sine and cosine functions are used to derive a position in the cartesian plane relative to the position of the previous digit (see code below for more details). As the irrational number is described to greater precision its decimal place increases, this occurs on the number string from left to right. As we are traversing the number sequence this corresponds to increasing time steps of the number analysis. On the plots the sequence position of the digit (its decimal place) is colour coded using a heat mapping (blue->red on increasing significant digits). The 3D plots also gives the sequence position of the digit on the Z axis, this helps to separate overlapping sequences in cartesian space.

Visualisation/Results

These plots are the results of the analysis, please click them for more detail

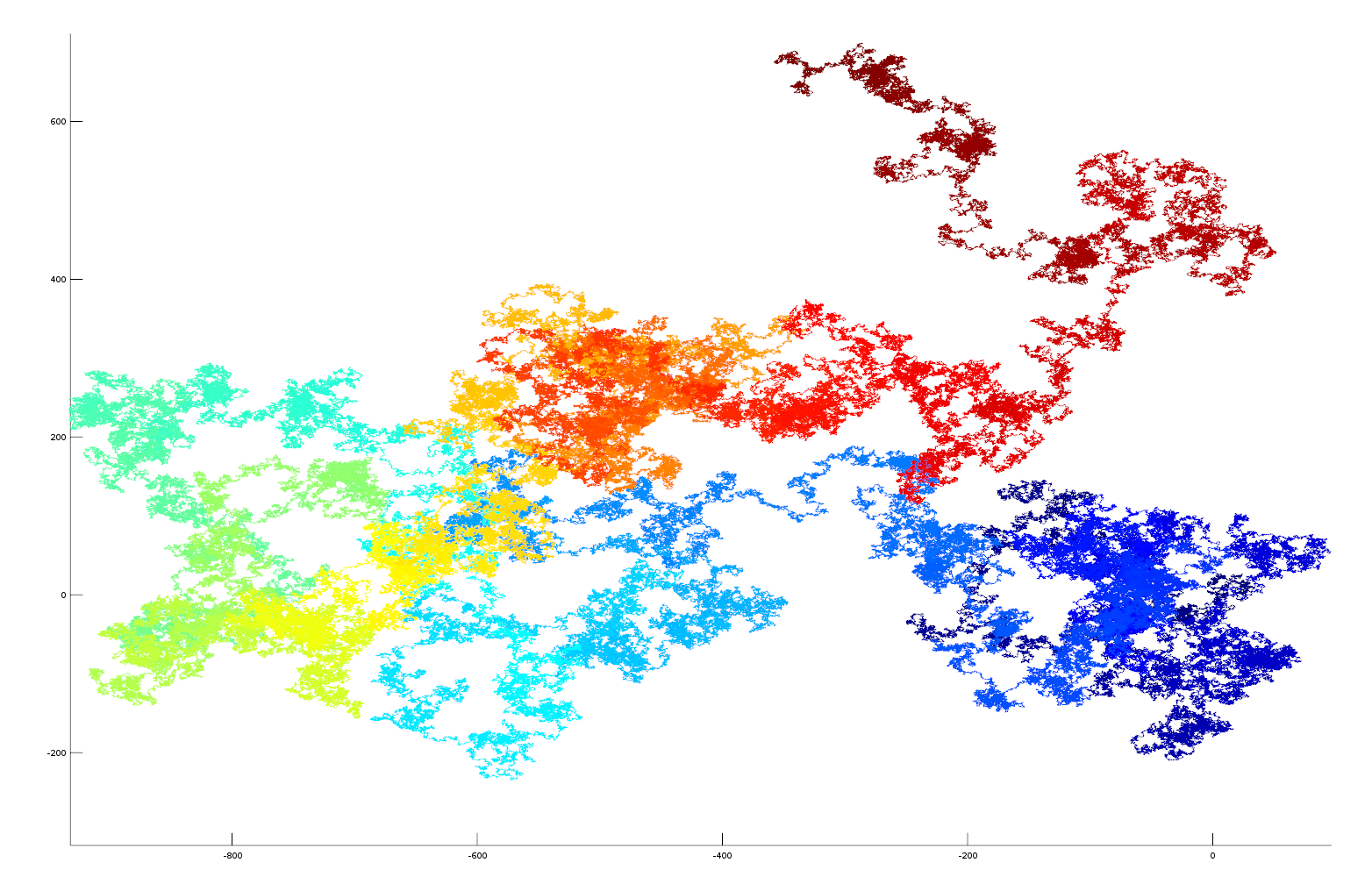
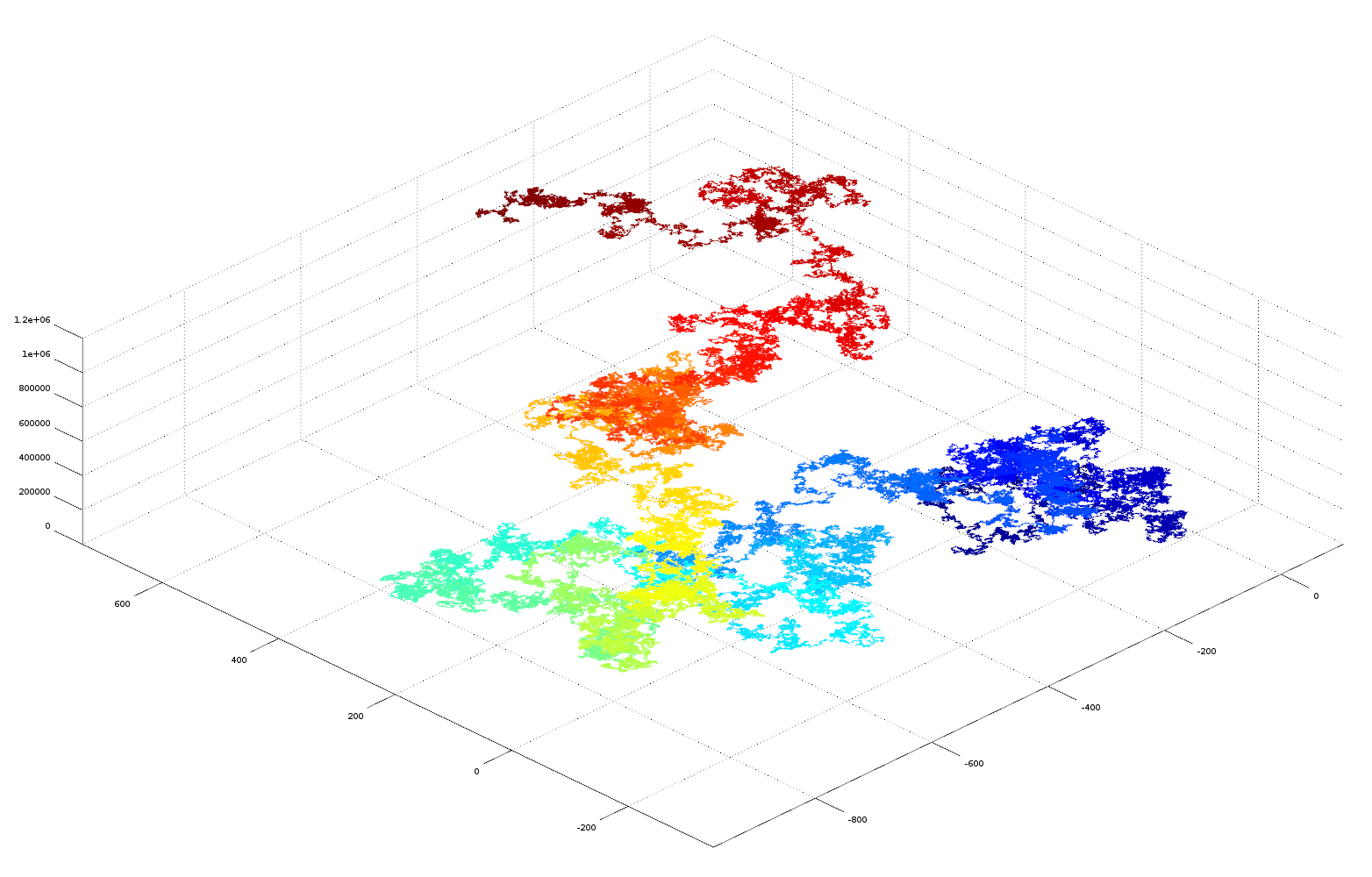
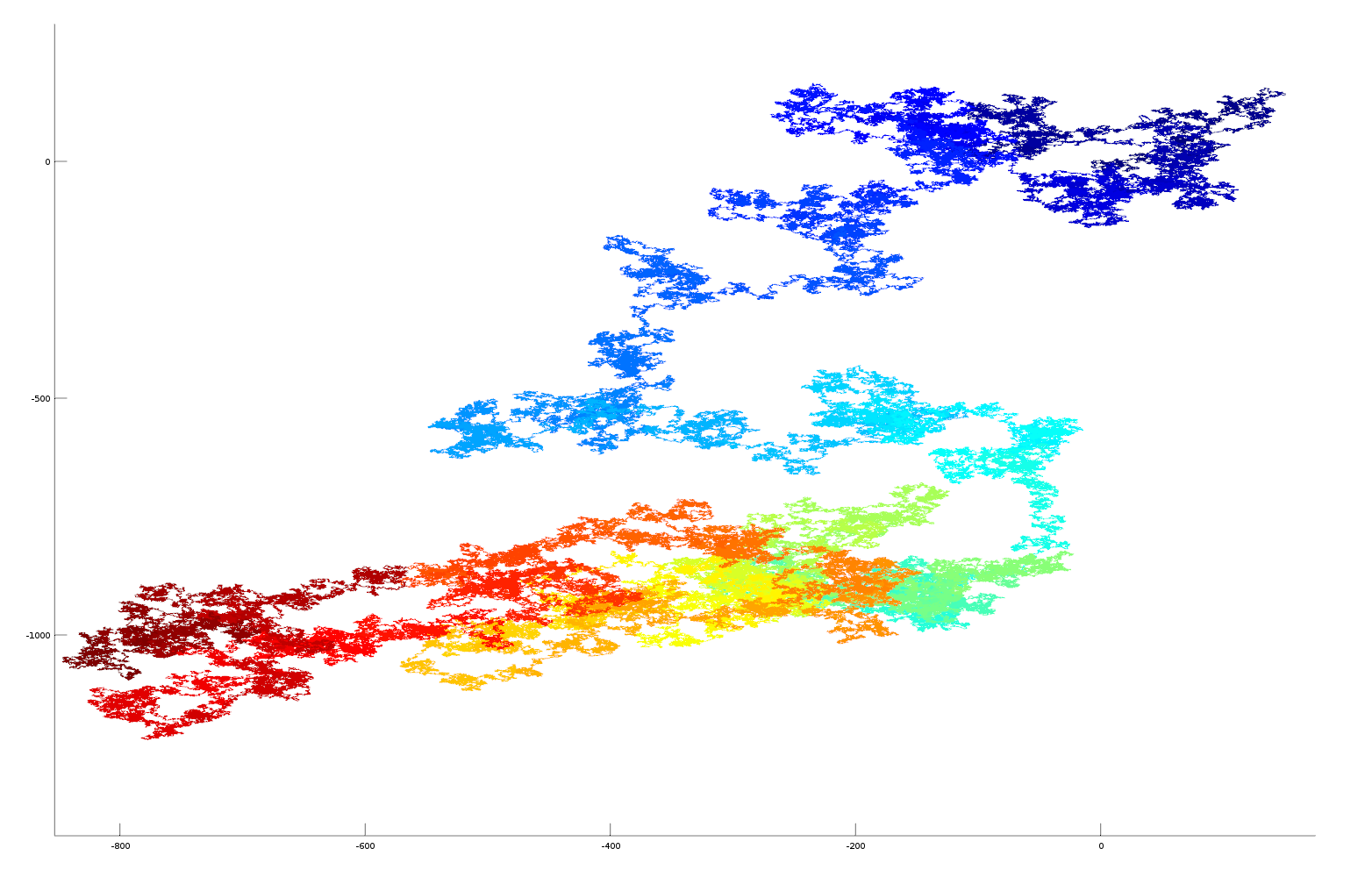
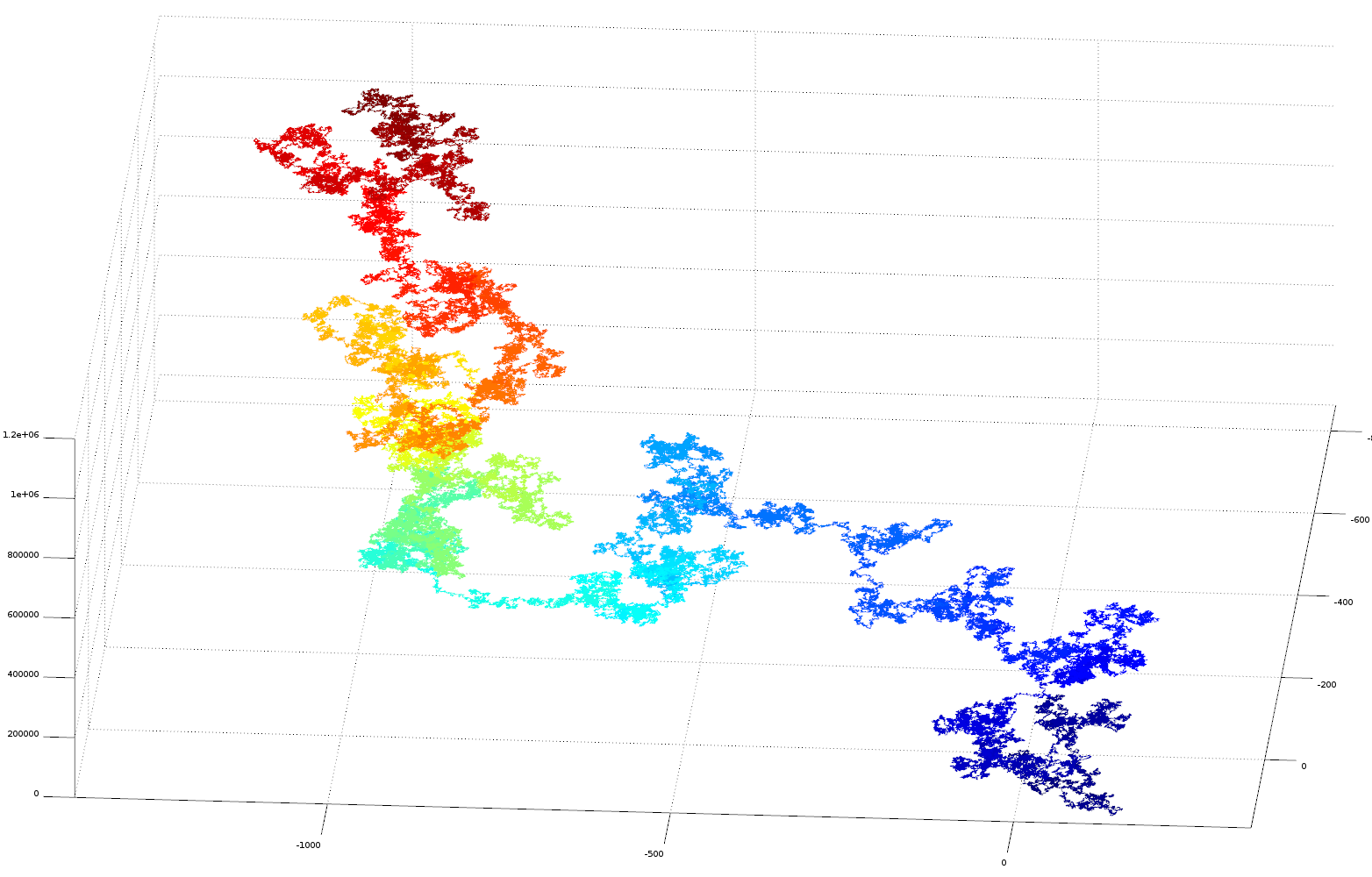
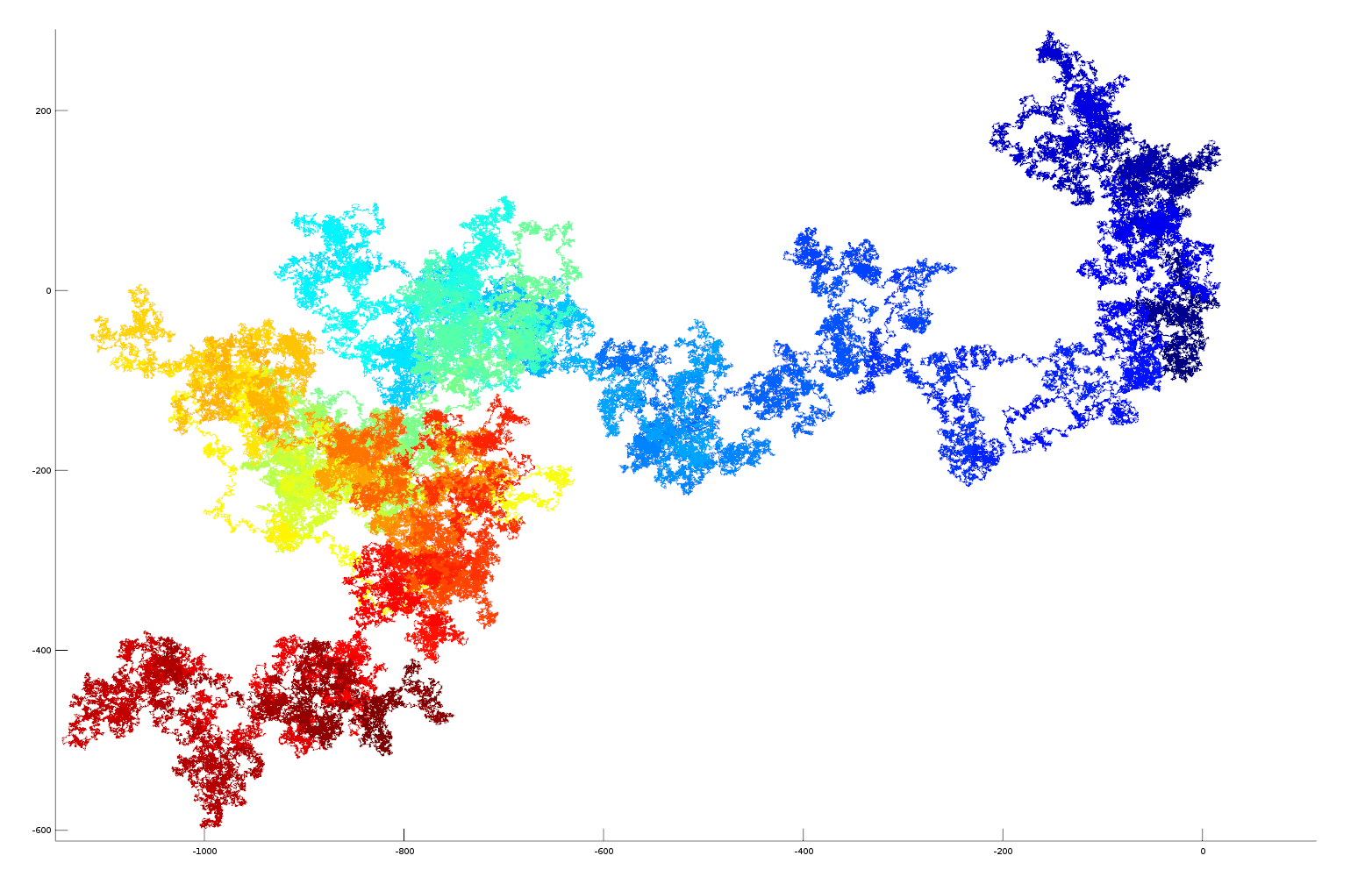
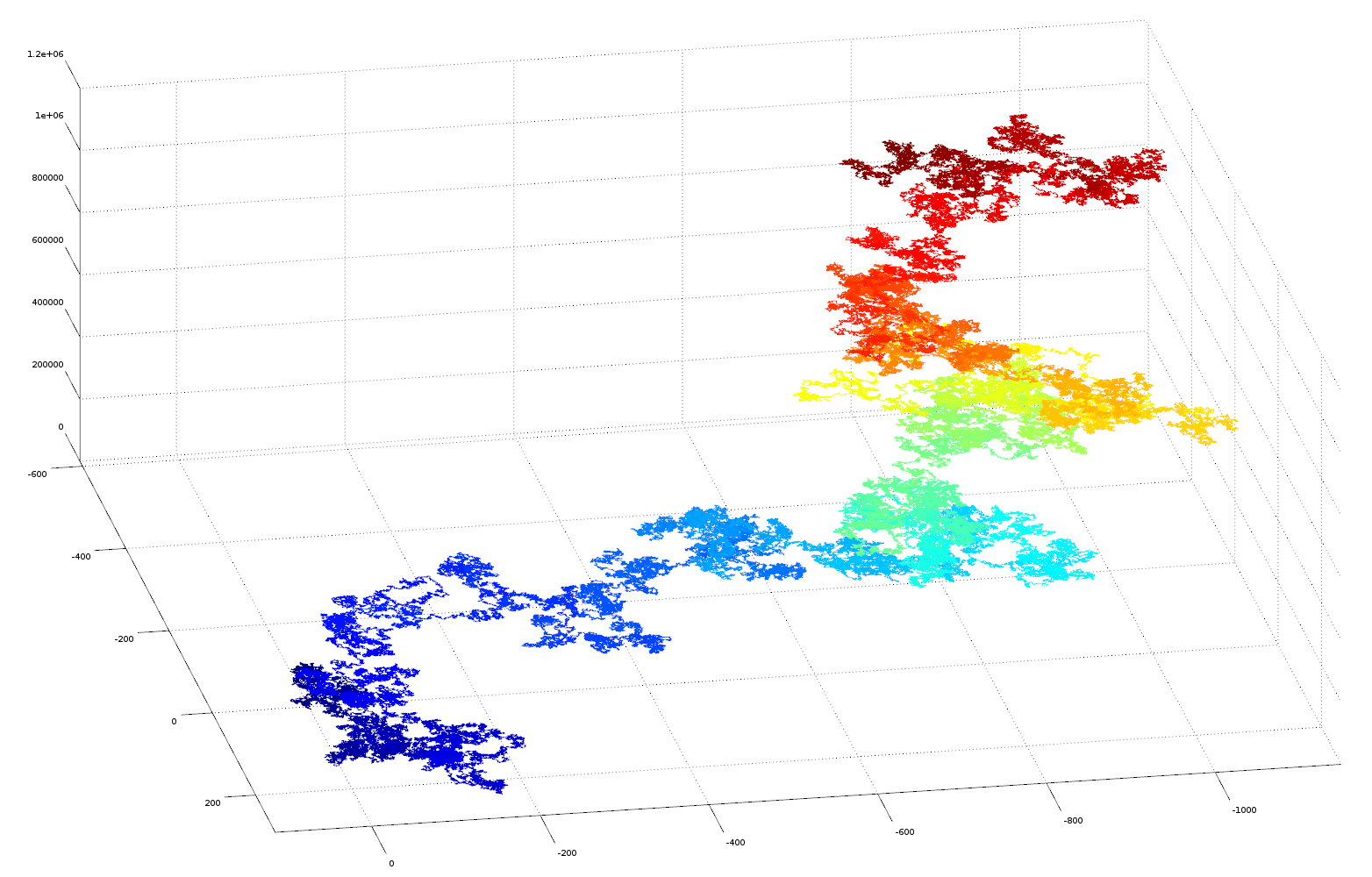
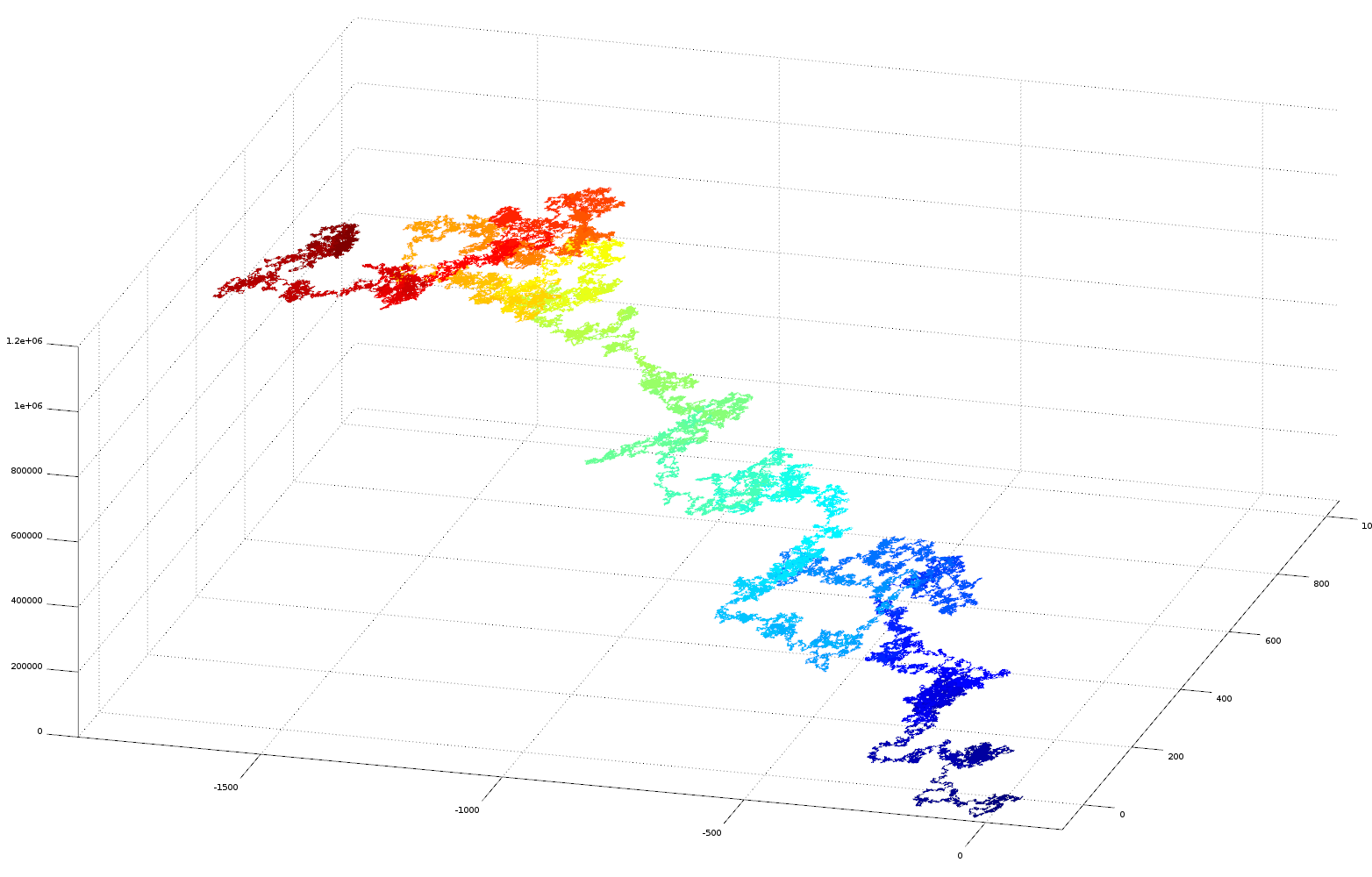
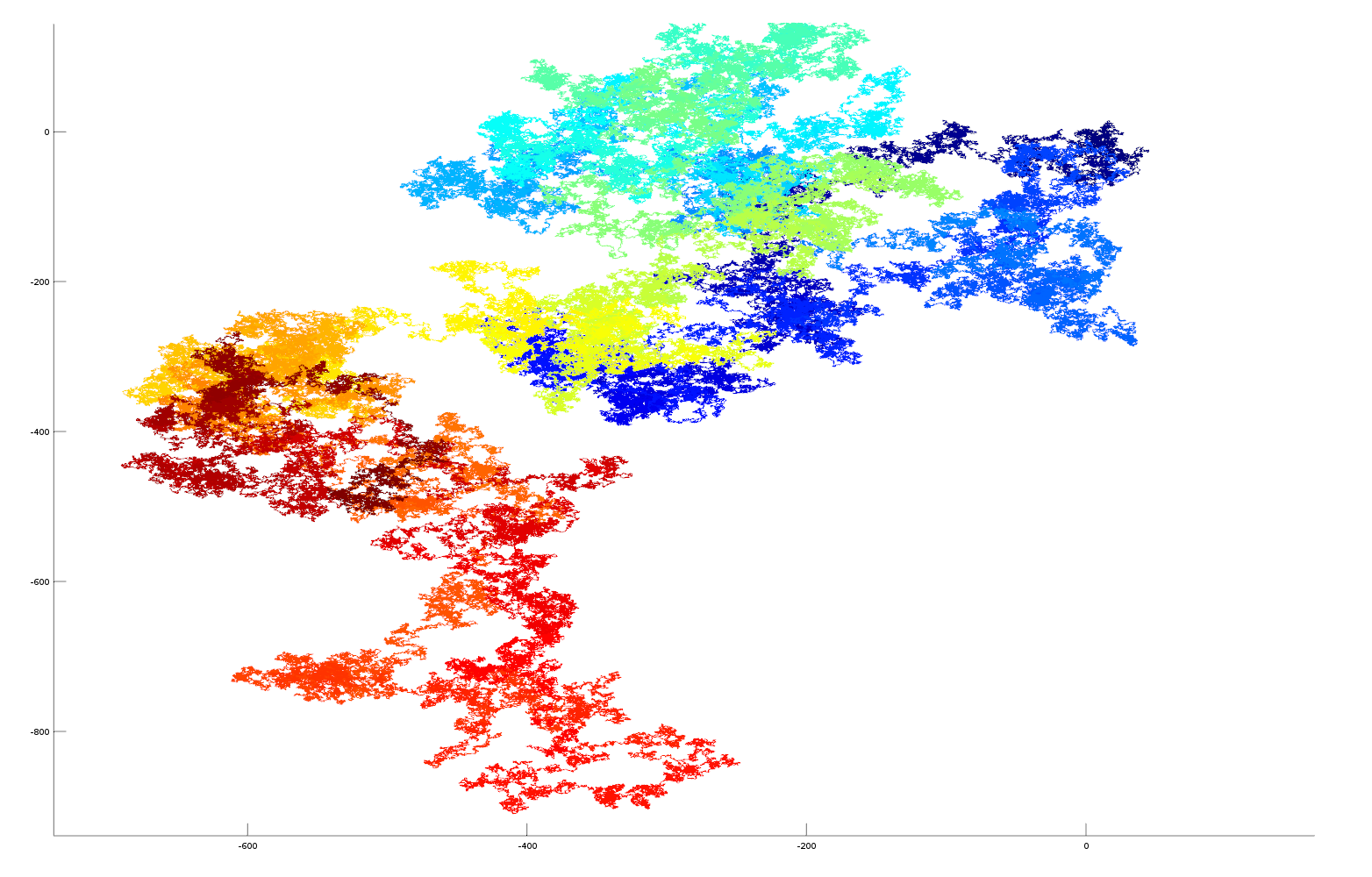
Here is a vector plot of 1 million random number generated numbers

Data and Matlab/Octave computer code

Below is the Matlab/Octave code used for generating the plots. Data can be downloaded here: pi, e, golden ratio, sqrt2 (data is without decimal point!)

function  irrational_number_plot_as_vector(filepathname)
%   requires file name containing string of irrational number delete decimal point from string ie 3.14... -> 314... 

% read text file containing number
format = "%1c"

fileID = fopen('pi.txt','r');

p = fscanf(fileID, format);

_p=0;

% convert character string to matlab array
for i=1:length(p); _p(i)  = str2double(strcat(p(i),".0")); end

% create arrays for plotting
x_array = zeros(1,length(_p));
y_array = zeros(1,length(_p));

% polar angle
for i=2:length(_p); x_array(i) = x_array(i-1)+cos((_p(i-1)/10.0)*2.0*pi); y_array(i) = y_array(i-1)+sin((_p(i-1)/10.0)*2.0*pi); end

% surface plot with z axis and colour blue->red as increased fractional part
h = surface([x_array(:), x_array(:)], [y_array(:), y_array(:)], [[1:length(_p)]', [1:length(_p)]'], [[1:length(_p)]', [1:length(_p)]'], 'EdgeColor','flat', 'FaceColor','none');

end

For real world vision or Robotic operations it is sometimes necessary to transform between coordinates in different coordinate systems. In this tutorial we will transform a 3D spiral from one coordinate system to another. The coordinate systems are specified in terms of their position in Cartesian space and converted to a vectorial representation.

First let us create and display the spiral

t = 0:pi/50:10*pi;
st = sin(t);
ct = cos(t);

The spiral is in 3D but we need a 4D matrix to perform the matrix transformations, so we also add a row of ones to it

spiral = [st; ct; t; ones(501,1)']

Ok, lets plot the relevant data

plot3(spiral(1,:), spiral(2,:), spiral(3,:), 'b')

we use the hold on command to keep plotting to the same chart

hold on

We are going to translate this spiral from its world coordinates to another local coordinate system

the coordinates are specified by a matrix = [X1, X2, X3, Y1, Y2, Y3, Z1, Z2, Z3]

world = [1,0,0;0,1,0;0,0,1]
local = [3,6,3;3,3,6;3,3,0]

The 3,3,0 in the last row (Z axis) of the matrix creates a 45 degree plane

Lets turn our local coordinate system into a vector

local_vector = zeros(3,3)
local_vector(:,1) = local(:,2)-local(:,1)
local_vector(:,2) = local(:,3)-local(:,1)
local_vector(:,3) = cross(local_vector(:,1),local_vector(:,2))

The vectors should be normalised to unit length like our world vector is

local_vector(:,1) = local_vector(:,1)/norm(local_vector(:,1))
local_vector(:,2) = local_vector(:,2)/norm(local_vector(:,2))
local_vector(:,3) = local_vector(:,3)/norm(local_vector(:,3))

Now we have to create our transform matrix using the dot product between our world and local vectors, this sets up the skew, reflection, rotation elements

transform = zeros(4,4)
transform(1,1) = dot(world(1,:), local_vector(1,:))
transform(1,2) = dot(world(1,:), local_vector(2,:))
transform(1,3) = dot(world(1,:), local_vector(3,:))
transform(2,1) = dot(world(2,:), local_vector(1,:))
transform(2,2) = dot(world(2,:), local_vector(2,:))
transform(2,3) = dot(world(2,:), local_vector(3,:))
transform(3,1) = dot(world(3,:), local_vector(1,:))
transform(3,2) = dot(world(3,:), local_vector(2,:))
transform(3,3) = dot(world(3,:), local_vector(3,:))

we also add the translated origin of our coordinate system to the last column of the matrix, this performs the X,Y,Z translation

transform(1,4) = local(1,1)
transform(2,4) = local(2,1)
transform(3,4) = local(3,1)
transform(4,4) = 1

So using our transform we can rotate the spiral by 45 degrees and translate it by 3 in X and 3 in Y

tspiral = transform*spiral;

let’s plot it in green next to the original spiral

plot3(tspiral(1,:), tspiral(2,:), tspiral(3,:), 'g')

(you might want to rotate the plot axis now to see the two spirals in 3D)

now to get it back again we use the inverse of our transformation matrix

tunspiralInv = inv(transform)*tspiral;

and plot it using markers so we can see the orginal spiral beneath

plot3(tunspiralInv(1,:), tunspiralInv(2,:), tunspiralInv(3,:), ‘r*’)

The plot should look like this

For the mathematical details behind the transform, these MIT lecture notes provide an excellent explanation.

If you find the article useful, please feel free to post a link to it