How mortgages or loans companies make money from you
The reason for this article is that in the past (whilst living in the UK) I have moved location and bought another house somewhere else like many people do. The mortgage company or bank said that they must cancel the mortgage and take out a new mortgage on the new house. It surprised me how little money I received back from the bank for the old mortgage for all those months that I had paid X hundreds of pounds paying back the mortgage (excluding the additional penalties for early termination!). So this article is going to look at the mortgage payments and give a few plots to illustrate what happens with your money.
In our mortgage example we are going to borrow 140,000 pounds at an interest of 6.5% annually for a term lasting 30 years. The main calculation will be how much of the principal (amount borrowed is paid back every month). For this we will use the annuity formula, where `r` is the monthly interest rate expressed as a decimal (`r`=yearly_rate/12/100), `P` is the principal or the amount borrowed and `N` the number of months in the full term.
`c=(r*P)/((1-(1+r)^-N))`
Using this formula we can calculate our monthly payment (c=885 pounds). The other formula we need is for the debt schedule which tells us how much of the principal gets paid off every month which we will term `p`.
`p=((1+r)*P’)-c`
Where `P’` is the previous months outstanding amount (`p`) which at the beginning of the term will be equal to `P` (More information on the formulas used can be found here).
I have generated a few plots from the formulas given above to try to demonstrate what happens to your money when you pay back a mortgage or loan. For example the plot of `p` vs `N` below shows a typical repayment curve for the borrowed money
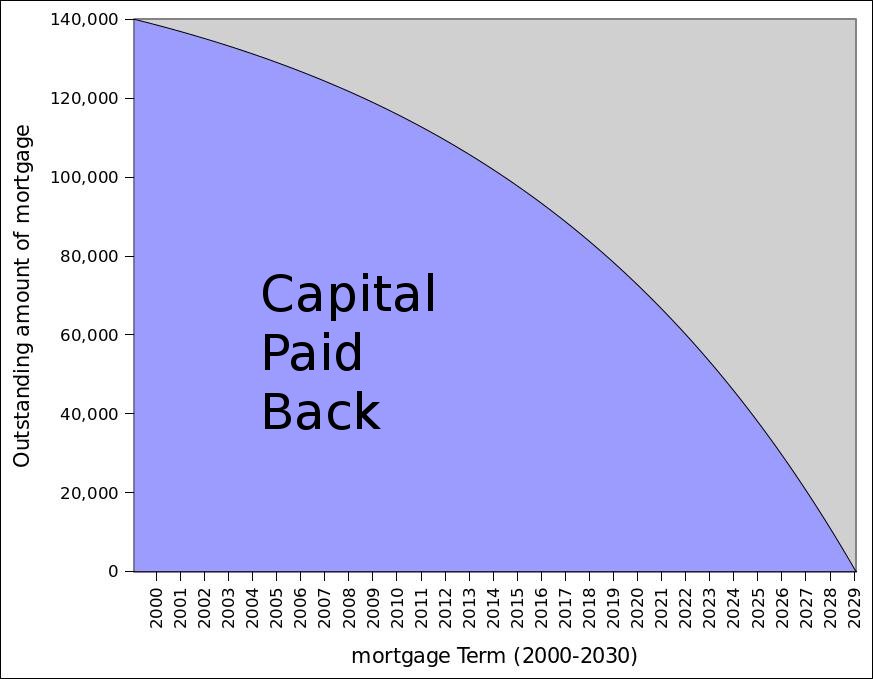
You can see in this figure that the amount of the capital that you pay back in the beginning years is not much with most of the money being spent paying back the interest. This means that if you move early on in the term you wont get much money back from the mortgage, therefore it is better if possible to hang in there until the full term has ended.
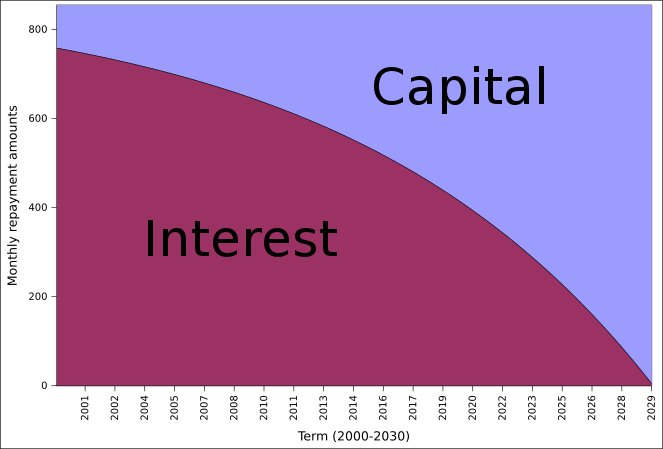
The next figure shows the proportions of the monthly mortgage payment split between capital and interest payments as the mortgage progresses. It actually takes 19 years 4 months before capital payments are greater than the interest payments in a 30 year mortgage.
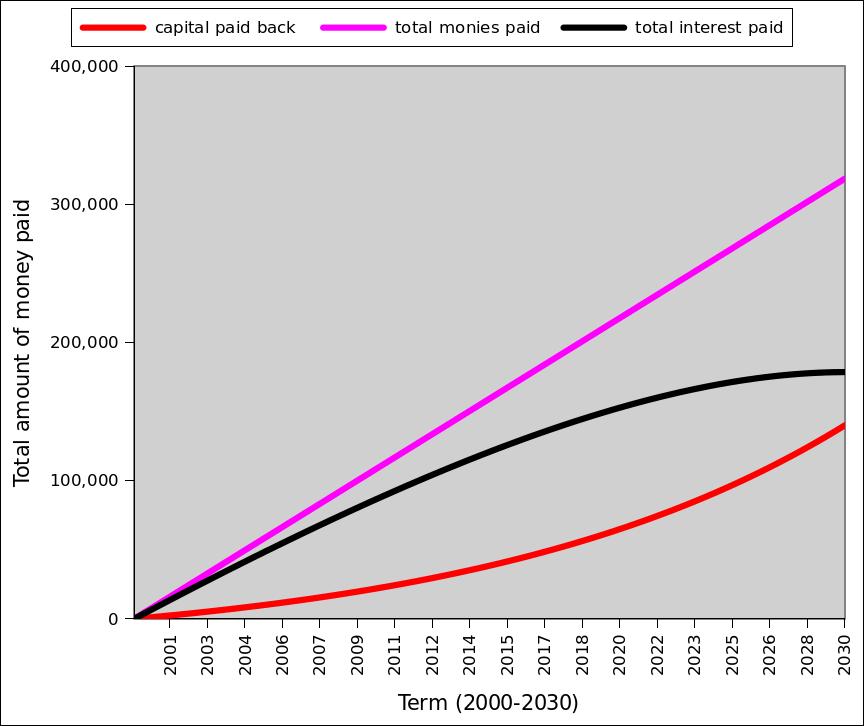
The final figure shows just how much extra money is made from lending the money and which proportion of this is interest or capital repayment. You actually pay more money towards interest than you do towards capital and the total money spent during the mortgage term is more than double the money borrowed.
Thank you Wikkipedia, Gnumeric and MathJax